1. 사각형의 정의
네 개의 선분으로 둘러싸인 도형을 사각형이라 한다 이때 사각형을 이루는 선분을 변이라고 하고 변과 변이 만나는 점을 꼭짓점이라 한다 사각형은 변과 꼭짓점이 각각 4개인 도형이다 그러나 4개의 선분이라 해도 도형의 일부가 끊어져 있거나 선분이 아닌 곡선이거나 선분이 서로 교차하면 사각형이라 하지 않는다

2. 사각형의 종류
사각형 중 네 각이 모두 직각인 사각형을 직사각형이라 한다 이도형은 네 각이 모두 직각이고 마주 보는 두변의 길이가 서로 같다 그리고 네 각이 모두 직각이고 네 편의 길이가 모두 같은 사각형을 정사각형이라 한다 직사각형과 정사각형의 마주 보는 변은 모두 평행하다 사각형은 마주 보는 변이 평행했는지 아닌지 마주 보는 평행한 변이 모두 몇 개인지에 따라 이름이 달라진다. 한쌍이 평행하면 사다리꼴이라 하고 두 쌍 모두 평행하면 평행사변형이라 한다 평행사변형은 두 쌍이 평행하므로 사다리꼴이라고도 할 수 있다 네변의 길이가 모두 같은 사각형을 마름모라고 한다. 이때 네변의 길이가 같은 정사각형은 마름모라고 할 수 있지만 마름모는 네 각이 직각이 아니므로 정사각형이라고 할 수 없다.
1. 사다리꼴 :평행한 변이 한쌍이라도 있는 사각형을 사다리꼴이라고 한다
2. 평행사변형 : 마주 보는 두 쌍의 변이 서로 평행한 사각형을 평행사변형이라 한다. 마주 보는 두 쌍의 서로 평행하므로 사다리꼴이라 할 수 있다 마주 보는 변의 길이가 같고 각의 크기가 같다 그리고 이웃한 두 각의 크기의 합이 180도이다
3. 마름모 : 네변의 길이가 모두 같은 사각형을 마름모라고 한다 마주 보는 두 쌍의 변이 서로 평행하고 크기가 같다
4. 직사각형 : 네 각이 모두직각이며 마주 보는 두 쌍의 변의 길이가 서로 같다 마주보는 두쌍의 변이 서로 평행하므로 평행사변형, 사다리꼴이라고 할 수 있다.
5. 정사각형 : 네 각이 모두 직각이고 네변의 길이가 모두 같다 마주 보는 두 쌍의 변이 서로 평행하다 정사각형은 네 각이 모두 직각이므로 직사각형이라고 할 수 있고 네변의 길이가 모두 같으므로 마름모라고 할 수도 있다.




3. 사각형의 높이
사각형의 높이는 평행한 두변 사이의 수직인 거리를 말한다. 사각형 중에서 평행한 두 변이 없는 사각형은 높이를 일정하게 정할 수 없다 또 사각형 중에서 평행한 변이 한쌍일 때는 높이도 한 가지로 정해질 수 있지만 평행한 두 변이 두 쌍일 때는 밑변의 위치에 따라 높이가 달라질 수 있다
4. 사각형의 포함관계
1. 평행사변형의 포함관계 : 평행사변형은 마주 보는 두 쌍의 변이 모두 평행하므로 사다리꼴이라고 할 수 있다 그러나 사다리꼴은 한쌍의 변만 평행하므로 평행사변형이라고 할 수는 없다.
2. 마름모의 포함관계 : 마름모는 네변의 길이가 같고 마주 보는 두 쌍의 변이 모두 평행하므로 평행사변형 사다리꼴이라고 할 수 있다 그러나 평행사변형과 사다리꼴은 네변의 길이가 같지 않으므로 마름모라고 할 수 없다
3. 직사각형의 포함관계 : 직사각형은 네 변이 모두 직각이고 마주 보는 두 쌍의 변이 모두 평행하므로 평행사변형 사다리꼴이라고도 할 수 있다 그러나 평행사변형과 사다리꼴은 네 각이 모두 직각이 아니므로 직사각형이라고 할 수 없다
4. 정사각형의 포함관계 : 정사각형은 네변의 길이가 모두 같고 네 각이 모두 직각이며 마주보는 두변의 길이가 같으므로 마름모 직사각형 평행사변형 사다리꼴이라고 할수있다 그러나 마름모는 네각이 모두 직각이 아니고 직사각형은 네변의 길이가 모두 같지 않으므로 평행사변형과 사다리꼴은 네변 길이가 같지 않고 네 각도 모두 직각이 아니므로 정사각형이라고 할 수 없다

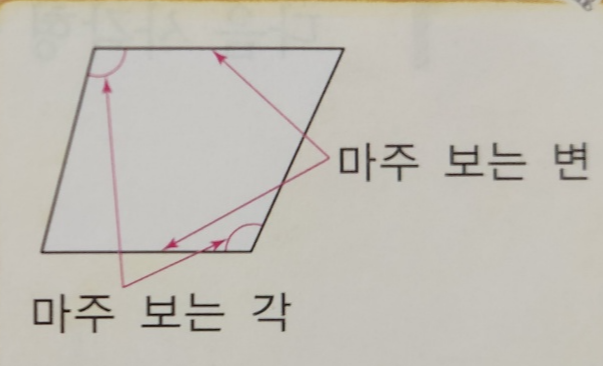

5. 마주 보는 변의 길이가 같은 사각형
사각형 중에서 마주 보는 변끼리 길이가 같은 도형은 평행사변형, 마름모, 직사각형, 정사각형이다. 이중에서 평행사변형과 직사각형은 마주보는 두변의 길이가 같고 마름모와 정사각형은 네변의 길이가 모두 같다
6. 마주 보는 각의 크기가 같은 사각형
사각형중에서 마주보는 각의 크기가 같은 도형은 평행사변형, 마름모, 직사각형, 정사각형이다. 이중에서 마주보는 두 각의 크기가 각각 같은 도형은 평행사변형과 마름모이고 네 각이 모두 직각으로 같은 도형은 직사각형과 정사각형이다.
7. 사각형의 네 각의 크기 합
사각형을 가위로 잘라 네 각을 맞추어 보면 4개의 각이 빈틈없이 원모양이 된다 따라서 사각형의 네 각의 크기의 합은 360도라는 것을 알 수 있다 또 사각형을 2개의 삼각형으로 나누어지는데 삼각형의 세 각의 크기의 합은 180도이므로 삼각형 2개로 나눈 사각형의 각의 합은 360도이다
'수학개념' 카테고리의 다른 글
| 시각과 시간 (0) | 2023.09.28 |
|---|---|
| 측정 - 길이 넓이 둘레 들이 무게 부피 (0) | 2023.09.28 |
| <수학상자> 길이의 단위 알아보기 (0) | 2023.09.28 |


