고1문제풀이(집합)

< 문제1 >

두 집합 A = {a,b,c}, B = {ab,bc,ca}에 대하여 A = B이고 a+b+c=-3일때, a³+b³+c³의 값을 구하시오.( 단, abc≠0 )

 

문제1풀이

< HELP 개념 >

문제관련개념

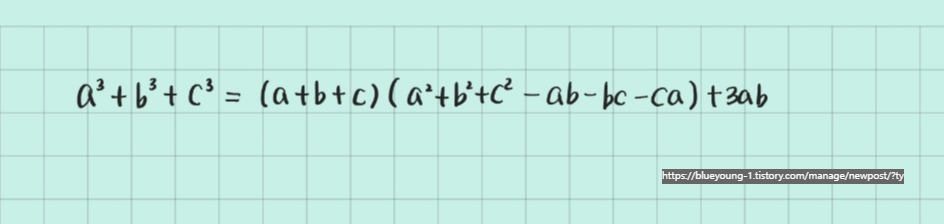
< 문제2 >

집합A = {1,2,3,···,n}의 부분집합 중 1,2는 반드시 원소로 갖고 3,4는 원소로 갖지 않는 부분집합의 개수가 16일때, 자연수 n의 값을 구하시오.

 

문제2풀이

< HELP 개념 >

문제관련개념

< 문제3 >

두집합 A={x|x²-4x+3=0}, B={x|x=2k-1,k=1,2,3,4,5}에 대하여 A⊂X⊂B, n(X) ≥ 3인 집합 X의 개수를 구하시오

 

문제3풀이

< 문제4 >

집합 A={2, 3, 4, 5}의 공집합이 아닌 서로 다른 15개의 부분집합을 각각 A₁, A₂, A₃, · · · , A₁₅라하고  A₁의 원소중에서 최소인 원소를 a₁, A₂ 의 원소중에서 최소인 원소를 a₂, · · · , A₁₅의 원소중에서 최소인 원소를 a₁₅라할때,  a₁ +  a₂ + · · · +  a₁₅ 의 값을 구하시오.

 

문제4풀이