2학기 중간고사 서술형 대비문제
1. 서술형 1번 문제
어느 학교 학생 60명에게 두 권의 책 A, B를 읽었는지 조사하였다. A를 읽은 학생은 35명, B를 읽은 학생은 45명이었다
A와 B를 모두 읽은 학생수의 최댓값을 M, 최솟값을 m이라 할 때, M - m의 값을 구하는 풀이과정과 정답을 서술하시오
< 풀이 >
n( A ∪ B) = n(A) + n(B) - n( A ∩ B )
n( A ∪ B) = 35 + 45 - n( A ∩ B )
60 = 80 - n( A ∩ B )
A ,B 모두 읽은 학생이 최대 35명까지 될 수 있으므로 35명이 최댓값이 될 수 있다
60 = 80 -20이므로 A ,B모두 읽은 학생이 최소 20명 될 수 있으므로 최솟값이 20이 된다
그러므로 M = 35, m = 20
∴ M - m = 15
< HELP 개념 >
n( A ∪ B) = n(A) + n(B) - n( A ∩ B )
2. 서술형 2번 문제
집합 X = { x ∣ x ≤ k } 에서 집합 Y = { y ∣ y ≥ k + 3 }으로의 함수 f(x) = x² - x가 일대일 대응일 때, 상수 k의 값은?
< 풀이 >
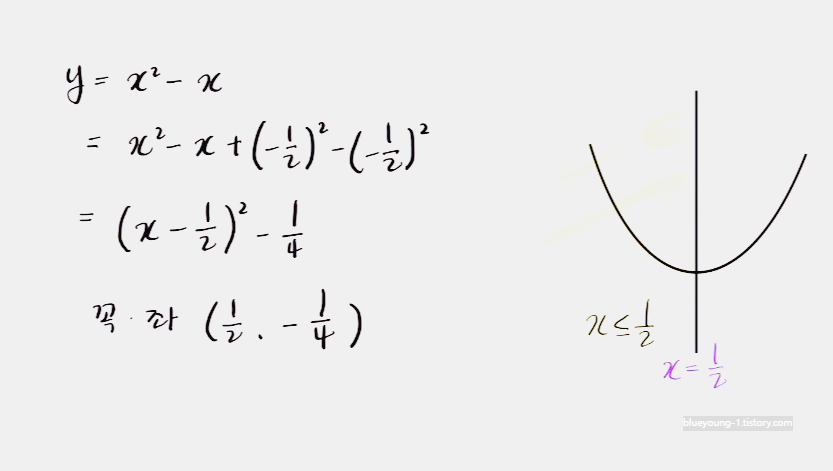
x가 ½ 보다 작아야 조건에 맞는다 따라서 k ≤ ½ 이여야 한다
f ( x ) = x² - x k² - k = k + 3
k² - 2k - 3 = 0 ( k -3 )( k + 1) = 0
∴ k = 3, k = -1
k가 ½ 보다 작아야 하므로 만족하는 k 값은 -1이다 따라서
x ≤ -1, y ≥ 2가 되므로 일대일 대응을 만족하게 된다.
∴ k = -1
< HELP 개념 >
일대일대응이란 정의역의 원소가 공역의 원소에 하나씩 대응하여야 공역과 치역이 같아야 한다 이차함수 전체는 일대일 대응관계가 성립되지 않지만 위의 문제와 같이 범위가 주어진다면 일대일 대응도 가능하다
3. 서술형 3번 문제
어느 학급 40명의 학생을 대상으로 논리사고력 대회와 골든벨 대회 참가여부를 조사하였다 논리사고력 대회에 참가하는 학생이 20명, 골든벨 대회에 참가하는 학생이 17명이었다 두 대회에 모두 참가하는 학생이 10명 이상일 때 두 대회 중 적어도 한 대회에 참여하는 학생은 최대 a명이고 최소 b명이다 a - b의 값은?
< 풀이 >
전체 U, 논리사고력 대회 참가하는 학생 A , 골든벨 대회 참가하는 학생 B라 정하자
n(U) = 40, n(A) = 20, n(B) = 17 n( A ∩ B ) ≥ 10 (최소 10명 이상)
적어도 한 대회에 참여하는 학생이라는 것은 A만 또는 B만 또는 A, B 모두 다 참여한다는 뜻이다 그렇다면 두 대회 중 적어도 한 대회에 참여하는 최대수는
n( A ∪ B) = 20+ 17 - 10 = 27 = a
두 대회중 적어도 한 대회에 참여하는 최소수는
n( A ∪ B) = 20+ 17 - 17 = 20 = b
따라서 a = 27 , b = 20이므로 a - b = 7
∴ a - b = 7
< HELP 개념 >
n( A ∪ B) = n(A) + n(B) - n( A ∩ B )
4. 서술형 4번 문제
좌표평면 위의 두 점 A( -5, 0 ), B( 0, 10 )을 지나는 직선 l과 원 x² + y² = 5 위를 움직이는 점 P가 있다 점 P와 직선ㅣ사이의 거리를 d라 할 때, 나올 수 있는 자연수 d의 값을 모두 구하는 과정을 서술하시오
< 풀이 >
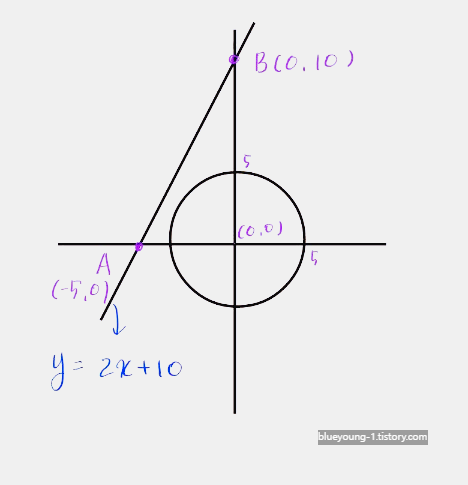
두 점 A( -5, 0 ), B( 0, 10 )을 지나는 직선 l는 y = 2x + 10이다. 2x - y +10 = 0 이므로 직선과 원 사이의 거리를 구하면 d = ∣ 10 ∣ / √5 = 2√5이다
M = 2√5 + √5 = 3√5 , m = 2√5 - √5 = √5
√5 ≤ d ≤ 3√5
√5는 2.xxx이고 3√5는 6.xxx 이므로 나올 수 있는 자연수는 d값은 3, 4, 5, 6이다
∴ d = 3, 4, 5, 6
< HELP 개념 >
원과 직선사이의 거리가 최대가 되려면 원의 중심과 직선사이의 거리에 반지름을 더하면 되고 원과 직선 사이의 거리가 최소가 되려면 원의 중심과 직선사이의 거리에 반지름을 빼주면 된다.
최대거리 = d + r , 최소거리 = d - r ( d = 원의 중심과 직선사이의 거리, r = 원의 반지름 )
'고등수학 > 고1' 카테고리의 다른 글
| 이차함수의 최대 최소 (0) | 2023.10.20 |
|---|---|
| 2학기 중간고사 서술형 대비 문제 (0) | 2023.10.19 |
| 원과 직선과의 관계 문제풀이 (0) | 2023.10.13 |
| 명제부정 문제풀이 (0) | 2023.10.09 |
| 명제 문제풀이 (0) | 2023.10.08 |



