정수와 유리수의 덧셈, 뺄셈, 곱셈, 나눗셈, 혼합계산

1. 정수와 유리수의 덧셈과 계산 법칙

(1) 부호가 같은 경우 : 두 수의 절댓값의 합에 공통인 부호를 붙인다.

(2) 부호가 다른 경우 : 두 수의 절댓값의 차에 절댓값이 큰 수의 부호를 붙인다.

(3) 세 수 a, b, c에 대하여 덧셈의 교환법칙과 결합법칙:a + b = b + a (교환법칙), (a + b) + c = a + (b + c) (결합법칙)

 +  +  +  = +(절댓값의 합),  -  + -  = -(절댓값의 합) /  +  +  -  ,  -  + +  →(절댓값이 큰 수의 부호)(절댓값의 차)

(4) 예제   

 

 

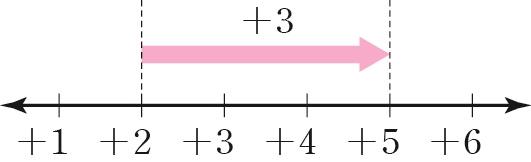
(+2)+(+3) = +(2+3) = +5

 

 

 

 

 

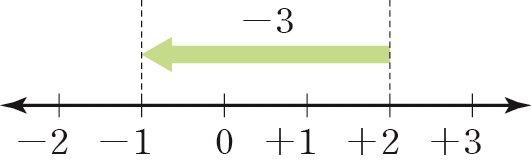
(+2)+(-3) = -(3-2) = -1

 

2. 정수와 유리수의 뺄셈 

정수와 유리수에서 뺄셈은 빼는 수의 부호를 덧셈으로 고친후 계산한다. -(+●) = +(-●) , -(-●) = +(+●)

3. 덧셈과 뺄셈의 혼합계산

(1) 부호가 표시되지 않은 수에는 + 부호를 붙인다.

(2) 빼는 수의 부호를 바꾸어 덧셈으로 고친다.

(3) 덧셈에 대한 교환법칙, 결합법칙을 이용하여 계산한다.

(4) 예제 :  6 - 13 + 15 = (+6)-(+13)+(+15) = (+6)+(-13)+(+15) = +8

 

4. 정수와 유리수의 곱셈과 계산법칙

(1) 부호가 같은 유리수의 곱셈 : 두 수의 절댓값의 곱에 + 부호를 붙인다.

(2) 부호가 다른 유리수의 곱셈 : 두 수의 절댓값의 곱에  - 부호를 붙인다.

(3) 세 수 a, b, c에 대하여 곱셈의 교환법칙, 결합법칙 : a × b=b × a(교환법칙), (a × b) × c = a × (b × c) (결합법칙)

(4) 세개 이상의 수에 곱셈 : 곱의 부호를 먼저 결정한후, 각 수들의 절댓값의 곱에 그 부호를 붙여서 계산한다. (음의 부호가 짝수개이면 +, 음의 부호가 홀수개이면 -를 붙여 계산한다.)

(5) 정수와 유리수의 거듭제곱 : 양수의 거듭제곱의 부호는 항상 양수이고, 음수의 거듭제곱의 부호는 지수가 짝수이면 +, 지수가 홀수이면 - 이다.

(6) 유리수 0의 곱은 항상 유리수이다.

 (+) × (+)  ,  (-) ×  (-)   →  + (절댓값의 곱)  /  (+) × (-)  ,  (-) ×  (+)   →  -  (절댓값의 곱)

 (-) × (-) ×·····×  (-) ×  (-)  → (+)   (-짝수개일때),  (-) × (-) ×·····×  (-) ×  (-)  → (-)   (-홀수개일때)

5. 정수와 유리수의 나눗셈

(1) 부호가 같은 두 유리수의 나눗셈 : 두 수의 절댓값의 몫에 + 부호를 붙인다.

(2) 부호가 다른 두 두 유리수의 나눗셈 : 두 수의 절댓값의 몫에 -부호를 붙인다.

(3) 역수를 이용한 나눗셈 : 역수란 두 수의 곱이 1이 될때, 한 수를 다른 수의 역수라고 한다.

 (+) ÷ (+)  ,  (-) ÷ (-)   →  + (절댓값의 몫)  /  (+) ÷ (-)  , (-)  ÷  (+)   →  -  (절댓값의 몫)

정수와 유리수의 곱셈처럼 (-)가 짝수개이면  부호가 (+)이고 (-)가 홀수개이면  부호가 (-)이다.

정수와 유리수 나눗셈 계산

6. 덧셈, 뺄셈, 곱셈, 나눗셈의 혼합계산 

(1) 혼합 계산의 순서

거듭제곱이 있으면 거듭제곱을 먼저 계산하고, 괄호가 있으면 소괄호, 중괄호, 대괄호 순으로 계산한다.((   ) → {    } → [   ]순우로 계산), 곱셈과 나눗셈은 앞에서 부터 계산한후 마지막으로 덧셈과 뺄셈을 앞에서부터 계산한다.

(2) 분배법칙 : 세수 a, b, c에 대하여 a×(b+c) = a×b + a×c, (a+b)×c = a×c + a×b

(3) 예제 : 55×(1000-3) = 55×1000 - 55×3 = 5500-165=5335

 

참고자료

 

정수와유리수덧셈.hwp

0.03MB

정수와유리수뺄셈.hwp

0.02MB

정수와유리수곱셈.hwp

0.03MB

정수와유리수나눗셈.hwp

0.03MB